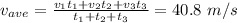Question

A record of travel along a straight path is as follows: 1. Start from rest with constant acceleration of 2.65 m/s2 for 17.0 s. 2. Maintain a constant velocity for the next 1.60 min. 3. Apply a constant negative acceleration of −9.39 m/s2 for 4.80 s.

(a) What was the total displacement for the trip?

b) What were the average speeds for legs 1, 2, and 3 of the trip, as well as for the complete trip

Answer 1

The total displacement for the trip is 4869.5705 m. Average speeds for legs 1, 2, and 3 are 22.525 m/s, 45.05 m/s, and 22.525 m/s respectively, while the average speed for the complete trip is 41.344 m/s.

Step-by-step explanation:

To determine the total displacement for the trip, we calculate each leg's displacement and sum them up:

Leg 1: Using the equation of motion s = ut + ½at² (where s is displacement, u is initial velocity, a is acceleration, and t is time), with initial velocity u = 0 m/s, acceleration a = 2.65 m/s², and time t = 17.0 s, the displacement for Leg 1 is s = 0 + ½(2.65)(17.0)² = 382.1225 m.

Leg 2: Convert 1.60 min to seconds: t = 1.60 min × 60 s/min = 96 s. The constant velocity v can be found by multiplying the acceleration in Leg 1 with the time of Leg 1: v = 2.65 m/s² × 17.0 s = 45.05 m/s. Thus, displacement for Leg 2 is s = vt = 45.05 m/s × 96 s = 4324.8 m.

Leg 3: Again using s = ut + ½at², with u = 45.05 m/s (from Leg 2), acceleration a = -9.39 m/s², and time t = 4.80 s, the displacement for Leg 3 is s = 45.05(4.80) + ½(-9.39)(4.80)² = 162.648 m.

The total displacement is the sum of the displacements from all three legs: 382.1225 m + 4324.8 m + 162.648 m = 4869.5705 m.

To determine the average speeds for each leg and the entire trip:

The average speed for Leg 1 is the final velocity divided by 2 since it started from rest: (0 + 45.05)/2 = 22.525 m/s.

The average speed for Leg 2 is simply the constant velocity: 45.05 m/s. The average speed for Leg 3 is also the initial velocity divided by 2 since it ends at rest: 45.05/2 = 22.525 m/s.

The average speed for the entire trip is the total distance divided by the total time: (382.1225 m + 4324.8 m + 162.648 m) / (17.0 s + 96 s + 4.80 s) = 4869.5705 m / 117.8 s = 41.344 m/s.

Answer 2

Hello

Let's solve the problem in the three different steps

1) Uniformly accelerated motion, with acceleration
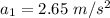
`a_1 = 2.65~m/s^2` and for a total time of
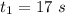
`t_1=17~s`. The body is initially at rest, so the distance covered is given by

`S= (1)/(2)a_1t_1^2=382.9~m`
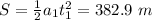
Calling
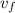
`v_f` and
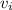
`v_i` the final and initial velocity, and since the
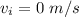
`v_i=0~m/s` because the body starts from rest, we can use

`a= (v_f-v_i)/(t)`
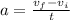
to find the final velocity after this first leg:

`v_(f)=v_i+a_1t_1=45~m/s`
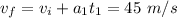
And the average velocity in this first leg is

`v_1= (v_f+v_i)/(2)=22.5~m/s`

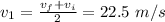
2) Uniform motion. The velocity is constant and it is equal to the final velocity of the first leg:
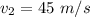
`v_2=45~m/s`. This is also the average velocity of the second leg.
The total time of this second leg is
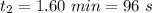
`t_2=1.60~min = 96~s`. The distance covered is given by

`S_2=v_2t_2=45~m/s \cdot 96~s=4320~m`

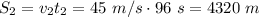
3) Uniformly decelerated motion, with constant deceleration of
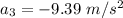
`a_3=-9.39~m/s^2` and for a total time of
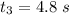
`t_3=4.8~s`. Here, the initial velocity of the body is the final velocity of the previous leg, i.e.
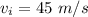
`v_i=45~m/s`. Therefore, the distance covered in this leg is given by

`S_3=v_i t_3 + (1)/(2) a_3 t^2 =107.8~m`
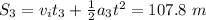
The final velocity in this leg is given by

`v_f=v_i+at=45~m/s-9.39~m/s^2 \cdot 4.8~s = -0.07~m/s`
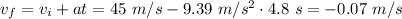
The negative sign means that after decelerating, the body has started to go in the opposite direction. Similarly to step 1, the average velocity in this leg is given by

`v_3 = (1)/(2)(v_f+v_i)= (1)/(2)(-0.07~m/s+45~m/s)= 22.5~m/s`

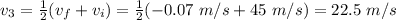
4) Finally, the total distance covered in the motion is

`S=S_1+S_2+S_3=382.9~m+4320~m+107.8~m=4810.7~m`
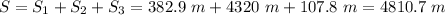
To find the average velocity, we must "weigh" the average velocity of each leg for the correspondent time of that leg:

`v_(ave)= (v_1t_1+v_2t_2+v_3t_3)/(t_1+t_2+t_3)=40.8~m/s`