Question

If an athlete leaps vertically at 4.0m/s, what maximum height does he reach?

Answer 1

Hello
This is a problem of accelerated motion, where the acceleration involved is the gravitational acceleration:
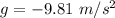
`g=-9.81~m/s^2`, and where the negative sign means it points downwards, against the direction of the motion.

Therefore, we can use the following formula to solve the problem:

`v_f^2 = v_i^2 + 2gS`
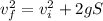
where
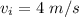
`v_i=4~m/s` is the initial vertical velocity of the athlete,
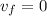
`v_f=0` is the vertical velocity of the athlete at the maximum height (and
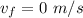
`v_f=0~m/s` at maximum height of an accelerated motion) and S is the distance covered between the initial and final moment (i.e., it is the maximum height). Re-arranging the equation, we get

`S= (v_f^2-v_i^2)/(2g)=0.82~m`