Answer:
Explanation:
Given that a certain element has a half life of 4.5 billion years.
For half life of 4.5 billion years we have the equation as
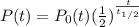
=
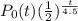 where t is in billions of years.
where t is in billions of years.
When P(t) = 35% of original we have
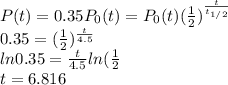
After 6.816 billion years.
-------------------------------
b) Here

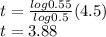
After 3.88 billion years.