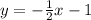Question

What is the equation, in point-slope form, of the line that is perpendicular to the given line and passes through the point (−4, −3)?

Answer 1

The given line is

`y=2x-3`

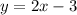
Notice that this equation is in slope-intercept form, where
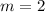`m=2` and
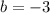`b=-3`, that is, its slope is 2, and its y-intercept is at -3.

Now, all perpendicular line to the given one must have a slope of -1/2, which is the opposite inverse number, and by definition that is the slope of a perpendicular line.

Then, we use the point-slope formula, using the slope and the given point

`y-y_(1) =m(x-x_(1) )\\y-(-3)=-(1)/(2)(x-(-4)\\ y+3=-(1)/(2)x+2\\ y=-(1)/(2)x-1`

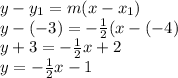
Therefore, the point-slope form is:
`y+3=-(1)/(2)(x+4)`

The point-intercept form is:
`y=-(1)/(2)x-1`

Answer 2

Answer: C ) y + 3 = 1/4 ( x + 4 )

Step-by-step explanation:

Given that you did not include the "given line", I can help you by explaning how to solve this kind of problems, step by step.

The procedure is based of the property of perpendicular lines: the product of the slopes of perpedicular lines is negative 1.

If you call m1, the slope of a line and m2 the slope of a perpendicular line, then:

m1 * m2 = - 1, and you can solve for either m1 or m2:

m1 = - (1 / m2)

m2 = - (1 / m1).

With that this is the procedure:

1) find the slope of the "given line". Name it m1.

2) find the slope of the perpendicular line:

m2 = - (1 / m1).

3) Use the equation of the line with the point (x1,y1) and slope m2

y - y1
-------- = m2
x - x1

4) In this case the point is (-4, - 3)=> x1 = - 4, y1 = - 3

=>

y - (-3)
---------= m2
x - (-4)

=> y + 3 = m2 * (x + 4)

=> y = m2*x + m2 * 4 - 3

Which is the point-slope form. You only have to replace m2 with the slope value of the perpendicular line, which I already explained that you find as m2 = (-1/m1).

Taking that the other line has m1 = - 4 so m2 = 1/4

y = (1/4)x + (1/4) * 4 - 3

y = (1/4) (x +4) - 3

y + 3 = (1/4) (x + 4) and answer is: C ) y + 3 = 1/4 ( x + 4 )