Answer:
domain is the set of all real values for x (-∞,∞)
Explanation:
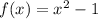 and
and
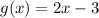
We need to find the domain of
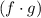
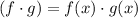
Plug in f(x) and g(x)
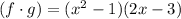
Multiply it using FOIL method
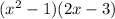
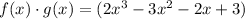
WE got an cubic equation, there is no restriction for x.
So domain is the set of all real values for x (-∞,∞)