Question

If f(x) = x2 – 1 and g(x) = 2x – 3, what is the domain of (f*g)(x)?

Answer 1

`(f.g)(x) =( f(x))(g(x)) \\ = ( {x}^(2) - 1)(2x - 3) \\ = (x - 1)(x + 1)(2x - 3)`
then the domain of (f•g)(x) is {-1, 1, 3/2}

Answer 2

domain is the set of all real values for x (-∞,∞)

Explanation:

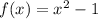`f(x) = x^2 -1` and
`g(x) = 2x - 3`

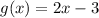
We need to find the domain of
`(f \cdot g)`

`(f \cdot g)=f(x) \cdot g(x)`

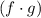
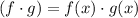
Plug in f(x) and g(x)

`(f \cdot g)=(x^2 -1)(2x-3)`

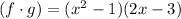
Multiply it using FOIL method

`(x^2 -1)(2x-3)`

`f(x) \cdot g(x)=(2x^3-3x^2-2x+3)`

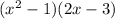
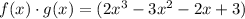
WE got an cubic equation, there is no restriction for x.

So domain is the set of all real values for x (-∞,∞)