Question

A balloon is filled with air at room temperature. It is then dipped into liquid nitrogen at 77K. Why does the balloon collapse

Answer 1

Because the air in the balloon is liquified by the cold temperature, and the air collapses to a very small volume of liquid.

Answer 2

This can be explained with the help of Charles law.

Charles law states that the volume of an ideal gas varies directly with its temperature in Kelvin.

The equation for the Charles law can be written as

`(V_(1))/(T_(1)) = (V_(2))/(T_(2))`

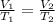
In the given example, V₁ is the initial volume of the gas

T₁ = Room temperature = 298 K

V₂ = Volume of gas in liquid nitrogen

T₂= 77 K

Let us plug in these values in Charles law equation.

`(V_(1))/(298 K ) = (V_(2))/(77K)`

`V_(2) = ((77K)(V_(1)))/(298K)`

`V_(2) = 0.26V_(1)`

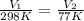
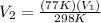
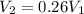
From the above , we can say that final volume (V₂) becomes almost a quarter of initial volume (V₁).

This happens because the temperature of liquid nitrogen is much lower than the room temperature and at lower temperature the gas occupies less volume

Therefore the balloon collapses when dipped in liquid nitrogen