Question

Each side of a square is increasing at a rate of 2 cm/s. at what rate is the area of the square increasing when the area of the square is 9 cm2?

Answer 1

Let x(t) = the length of a side of the square (cm) at time t (s).
The rate of change of x is given as

`(dx)/(dt) =2 \, (cm)/(s)`

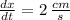
The area (cm²) at time t is
A = x²

The rate of change of the area with respect to time is

`(dA)/(dt) = (dA)/(dx) (dx)/(dt) =2 (dA)/(dx) =2(2x)=4x \, (cm^(2))/(s)`

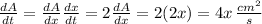
When A = 9 cm², then x = √9 = 3cm. Hence obtain

`(dA)/(dt) = 4(3) = 12 \, (cm^(2))/(s)`

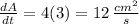
Answer: 12 cm²/s