Let x(t) = the length of a side of the square (cm) at time t (s).
The rate of change of x is given as
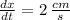
The area (cm²) at time t is
A = x²
The rate of change of the area with respect to time is
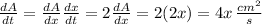
When A = 9 cm², then x = √9 = 3cm. Hence obtain
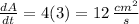
Answer: 12 cm²/s