1) The expression needs some parenthesis for fully understanding.
I will rewrite it in a way that does not permit doubts:
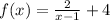
2) It might help you to know that it is the same that g(x-1)+4 being g(x) = 2 / x.
That helps becuase it means that the graph of f(x) is the graph of the function 2 / x shifted 1 unit to the right and 4 units upward.
3) Also, this will help to determine the graph of f(x):
- y-intercept: =>. x = 0 => f(0) = -2 + 4 = 2
- x - intercept (roots) => y = 0 => 0 = 2 / (x - 1) + 4 => x = 1/2
- domain: all real values - {1}
- vertical asymptotes: find the limit for when x approaches to 1. Given that it is infinite x = 1 is a vertical asymptote
- ending behavior: find the limits when x → +/- ∞.
It is 4, so y = 4 is horizontal asymptote for both extremes: f(x) appraches 4 for the two extremes without touching the line y = 4
- range all real values - {4}
- it does not have regional minima o maxima.
4) Finally do a table with some values.
I have attached a graph of the function, which you can understand and do by yourself with the information and explanations given above.