Question

When a pitcher is throwing a ball, is he applying positive or negative work to the ball?

A. Positive.

B. Negitive

Answer 1

A.Positive as work=force×distance (assuming that distance is always a constant) the work will always be positive as the force is always positive(this is because force=mass×acceleration where the acceleration is always positive unless the mass is being slowed down)

Answer 2

When a pitcher is throwing a ball, he is applying positive work to the ball.

Answer: Option A

Explanation:

According to work energy relation, the object's kinetic energy changes due to external force equal to work done.

Work done=Final kinetic energy-Initial kinetic energy

As the ball is thrown by the pitcher, the initial kinetic energy of the ball will be zero as the initial velocity of the ball is zero due to being at rest before being thrown by the pitcher.

After the ball is thrown, the final kinetic energy will be depending on the mass of the ball and the velocity at which the ball is thrown. We know that,

`\text {Kinetic Energy}=(1)/(2) * \text { mass of the object } * \text { (velocity of motion) }^(2)`

For final velocity,

`\text {Final kinetic energy}=(1)/(2) * m * v_(f)^(2)`

For initial velocity,

`\text { Initial kinetic velocity }=(1)/(2) * m * v_(i)^(2)=0`

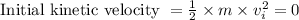
Thus,

`\text {Work done }=(1)/(2) * m * v_(f)^(2)-0=(1)/(2) * m * v_(f)^(2)`

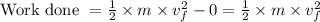
So, the work done on the ball is positive as the velocity increased from zero.