This is a classic example of conservation of energy. Assuming that there are no losses due to friction with air we'll proceed by saying that the total energy mus be conserved.

Now having information on the speed at the lowest point we can say that the energy of the system at this point is purely kinetic:
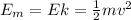
Where m is the mass of the pendulum. Because of conservation of energy, the total energy at maximum height won't change, but at this point the energy will be purely potential energy instead.
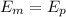
This is the part where we exploit the Energy's conservation, I'm really insisting on this fact right here but it's very very important, The totam energy Em was
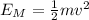
It hasn't changed! So inserting this into the equation relating the total energy at the highest point we'll have:
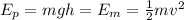
Solving for h gives us:
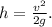
It doesn't depend on mass!