Question

The curved part of this figures is a semicircle.

What is the best approximation for the area of this figure?

28+16.25π units²

28+8.125π units²

14+16.25π units²

14+8.125π units²

Answer 1

The answer is 14+8.125π units².

Answer 2

Answer: 14+8.125π units²

Explanation:

By the given diagram,

The diameter of the semicircle = The line segment having the end points (-4,-2) and (3,2),

`=√((3+4)^2+(2+2)^2)`

`=√(7^2+4^2)`

`=√(49+16)`

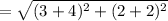
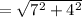
`=√(65)` unit,

Thus, the radius of the semicircle = √65/2 unit,

⇒
`\text{Area of the semicircle}=(1)/(2)\pi((√(65))/(2))^2`

`= (1)/(2)\pi((65)/(4))`

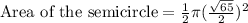
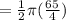
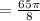`=(65\pi)/(8)` square unit.

Now, by the given diagram,

The area of the triangle having the vertices (-4,-2), (3,2) and (-4,2) ( By the coordinate form of area of a triangle formula )

`=(1)/(2)[-4(2-2)+3(2+2)-4(-2-2)]`

`=(1)/(2)* 28`

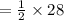
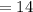`=14` square unit,

Hence, the total area of the given figure = Area of semicircle having diameter √65 + area of triangle having vertices (-4,-2), (3,2) and (-4,2)

`=(65\pi)/(8)+14`

`=(8.125\pi+14)` square unit.

⇒ Fourth option is correct.