Question

A single die is rolled twice find the probability of rolling an even number the first time and a number greater than 5 the second time

Answer 1

The probability is
`(1)/(12)` .

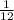To find the probability of rolling an even number on the first die and a number greater than 5 on the second die, we can consider the possible outcomes.

A standard six-sided die has the numbers 1 through 6.

Even number on the first roll: The even numbers on a die are 2, 4, and 6. So, there are 3 favorable outcomes.

Number greater than 5 on the second roll: The numbers greater than 5 on a die are 6. So, there is 1 favorable outcome.

Now, multiply the number of favorable outcomes for each roll:

P(Even on the first roll and >5 on the second roll)=P(Even on the first roll)×P(>5 on the second roll)

P(Even on the first roll and >5 on the second roll)=
`(3)/(6) * (1)/(6)`

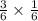
​Simplify the expression:

P(Even on the first roll and >5 on the second roll)=
`(3)/(36)`

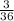
Reduce the fraction:

P(Even on the first roll and >5 on the second roll)=
`(1)/(12)`

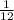
So, the probability is
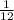`(1)/(12)` .

Answer 2

the probability of rolling of rolling an even number would be 3/6 because there are three even numbers out of six. If this were rolled twice, it'd be double (it'd become 6/12)
then the probability of rolling a number greater than five on the second turn would be 1/6 because only one number is greater than five on a die, which is six. Again, if it were rolled twice, it'd be double (and become 2/12)