The question isn't clear enough, I think it ask us to calculate the linear speed of a point at the edge of the DVD.
Now let's imagine we're a point at the edge of the DVD, we're undergoing a circular motion. Each minute we will complete a circular track 7200 times, now we need to know the distance we travel each turn. The perimeter of the DVD, a circular object is:
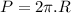
Know recall that:
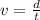
We now need to know how much distance is traveled during a minute or 60 seconds:
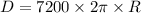
Finally we divide this result with t=60 seconds:

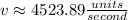
Where the distance units were named units as the length unit is not specified in this exercise.