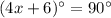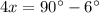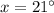Question

What is the value of x in the rhombus below?

Answer 1

Option C

`21\°`

Explanation:

we know that

The two diagonals of a rhombus are perpendicular

so

Let

O------> the center of the rhombus

m∠AOB=
`90\°`

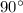
Remember that

The sum of the internal angles of a triangle is equal to
`180\°`

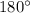
therefore

in the triangle AOB

m∠AOB+m∠OAB+m∠OBA=
`180\°`

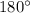
substitute the values

`90\°+(2x+1)\°+(2x+5)\°=180\°`

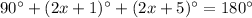
solve for x

`(4x+6)\°=90\°`

`4x=90\°-6\°`

`x=21\°`

Answer 2

Look into my attachment

in rhombus ABCD, ∠AOB = 90°

Look at ΔAOB
the sum of inner angles = 180°
∠BAO + ∠AOB + ∠ABO = 180°
2x + 1 + 90 + 2x + 5 = 180°
4x + 96 = 180
4x = 84
x = 21