Question

In a material for which o=5.0 S/m and e, =1 the electric field intensity is E- 250 sin 10" (V/m). Find the conduction and displacement current densities, and the frequency at they have equal magnitudes.

Answer 1

Step-by-step explanation:

Given that:

The conductivity of the material
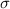`\sigma` = 5.0 s/m

`The \ relative \ permittivity \ of \ the \ material`
`{\varepsilon_r} = 1` ; &

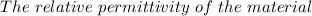
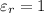The electric field intensity of the material E = 250 sin(10¹⁰ t) V/m

(a) The conduction current density
`( J_c) = \sigma E`

`= 5.0 * 250 \ sin ( 10^(10) \ t )`

`\mathbf{ = 1250 \ sin (10 ^(10) t ) \ A/m^2 }`

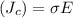
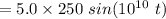
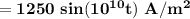
(b) Displacement current density
`(J_d) = \varepsilon _d * (\delta E)/(\delta t)`

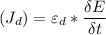
Recall that:

`\varepsilon _o = 8.854 * 10^(-12)`

∴

`(J_d) = 8.854 * 10^(-12) * (d)/(dt) * (250 \ sin \ (10^(10) \ t))`

`(J_d) = 8.854 * 10^(-12) * 250 * 10^(10) * \ cos \ (10^(10) \ t)`

`(J_d) = 22.135 \ cos \ 10^(10) \ t \ A/m^2`

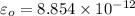
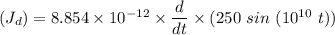
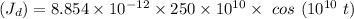
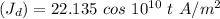
(c) The frequency at which
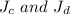`J_c \ and \ J_d` will have the same magnitude is:

`f = (\sigma)/(2 \pi \varepsilon_o \varepsilon_r)`

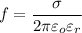
By substitution

`f = 18 * 10^9 * (\sigma )/(\varepsilon_r)`

`f = 18* 10^9 * (5)/(1 )`

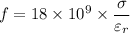
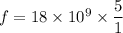
f = 90 GHz