Question

In 1998 the U.S. Hispanic high school dropout rate was 29.5% and in 2008 it had dropped to 18.3%. Let d represent the U.S. Hispanic high school dropout rate and y represent the years since 1990. Find a linear model for the dropout rate

Answer 1

d represent the U.S. Hispanic high school dropout rate
y represent the years since 1990.
The first thing we should do is find the equation of the straight line. For this we use the following table that we obtain from the data of the problem
y d
1998 29.5
2008 18.3
The linear model for the dropout rate is
d = -1.12y + 2267.3
answer
d = -1.12y + 2267.3

Answer 2

Since the model is linear, the function describing the U.S. Hispanic high school dropout rate (d) is given by:
d = A*y + B

Note that y represents the years counting from 1990, so 2008 will correspond to y=18, and 1998 to y=8

A is calculated through the formula:

`A= (d.final - d.initial)/(y.final - y.initial) = (18.3-29.5)/(18-8)=(-11.2)/(10)=-1.12`

So the dropout rate is, according to this model, diminishing 1.12% per year.
Now that we know A, we can calculate B simply by replacing the KNOWN values in the formula:

`d=A*y+B 18.3=-1.12*18+B B=18.3+1.12*18=38.46`

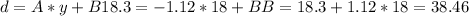
So the model states that

d=-1.12*y+38.46