Answer: 40%
Explanation:
Let A be the event that the athlete play baseball and B be the event that the athlete play basketball.
Given: The probability of athletes play baseball =
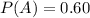
The probability of athletes play baseball and basketball =
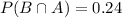
Then the probability that the athletes who play baseball also play basketball is given by :-
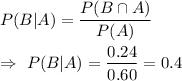
In percent ,
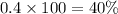
Hence, 40% of athletes who play baseball also play basketball.