Question

Based on the Fundamental Theorem of Algebra, how many complex roots does each of the following equations have? Write your answer as a number in the space provided. For example, if there are twelve complex roots, type 12.

x(x2 - 4)(x2 + 16) = 0 has complex roots

(x 2 + 4)(x + 5)2 = 0 has complex roots

x6 - 4x5 - 24x2 + 10x - 3 = 0 has complex roots

x7 + 128 = 0 has complex roots

(x3 + 9)(x2 - 4) = 0 has complex roots


how many complex roots does each have

Answer 1

The first equation is of degree 5 so has a total of 5 roots. It has 3 real roots
and 2 complex roots.
Second equation 2 complex roots.
Third has 4 complex roots
fourth has 7 complex roots
fifth has 3 complex roots

Answer 2

2, 2, 4, 6, 4

Explanation:

Fundamental Theorem of Algebra states that 'An 'n' degree polynomial will have n number of real roots'.

1. The polynomial is given by
`x(x^2-4)(x^2+16) = 0`

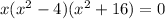
So, on simplifying we get that,
`x(x+2)(x-2)(x^2+16)=0`.

Since, degree of polynomial is 5, it will have 5 roots.

This gives us that the roots of the equation are x = 0, -2, 2, 4i and -4i

So, the number of complex roots are 2.

2. The polynomial is given by
`(x^2+4)(x+5)^2 = 0`

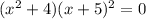
Since, degree of polynomial is 4, it will have 4 roots.

Equating them both by zero,
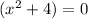`(x^2+4)= 0` and
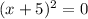`(x+5)^2=0` gives that the roots of the polynomial are x = 2i, -2i, -5, -5.

So, the number of complex roots are 2.

3. The polynomial is given by
`x^6-4x^5-24x^2+10x-3=0`

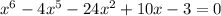
Since, degree of polynomial is 6, it will have 6 roots.

On simplifying, we get that the real roots of the polynomial are x = -1.75 and x = 4.28.

So, the number of complex roots are 6-2 = 4.

4. The polynomial is given by
`x^7+128=0`

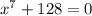
Since, degree of polynomial is 7, it will have 7 roots.

On simplifying, we get that the only real root of the polynomial is x = -2.

So, the number of complex roots are 7-1 = 6.

5. The polynomial is given by
`(x^3+9)(x^2-4)=0`

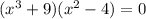
Since, degree of polynomial is 5, it will have 5 roots.

Simplifying the equation gives
`(x+2)(x-2)(x+\sqrt[3]{9})(x^2-\sqrt[3]{9x}+9^{(2)/(3)})=0`

Equating each to 0, we get the real roots of the polynomial is
`x=-3^{(2)/(3)}`

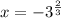
So, the number of complex roots are 5-1 = 4