Answer:
2, 2, 4, 6, 4
Explanation:
Fundamental Theorem of Algebra states that 'An 'n' degree polynomial will have n number of real roots'.
1. The polynomial is given by
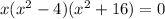
So, on simplifying we get that,
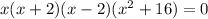 .
.
Since, degree of polynomial is 5, it will have 5 roots.
This gives us that the roots of the equation are x = 0, -2, 2, 4i and -4i
So, the number of complex roots are 2.
2. The polynomial is given by
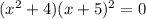
Since, degree of polynomial is 4, it will have 4 roots.
Equating them both by zero,
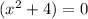 and
and
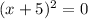 gives that the roots of the polynomial are x = 2i, -2i, -5, -5.
gives that the roots of the polynomial are x = 2i, -2i, -5, -5.
So, the number of complex roots are 2.
3. The polynomial is given by
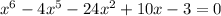
Since, degree of polynomial is 6, it will have 6 roots.
On simplifying, we get that the real roots of the polynomial are x = -1.75 and x = 4.28.
So, the number of complex roots are 6-2 = 4.
4. The polynomial is given by
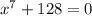
Since, degree of polynomial is 7, it will have 7 roots.
On simplifying, we get that the only real root of the polynomial is x = -2.
So, the number of complex roots are 7-1 = 6.
5. The polynomial is given by
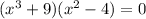
Since, degree of polynomial is 5, it will have 5 roots.
Simplifying the equation gives
![(x+2)(x-2)(x+\sqrt[3]{9})(x^2-\sqrt[3]{9x}+9^{(2)/(3)})=0](https://img.qammunity.org/2019/formulas/mathematics/high-school/7ej64hd49a29odortg6plflyjr6dnpjucw.png)
Equating each to 0, we get the real roots of the polynomial is
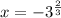
So, the number of complex roots are 5-1 = 4