Answer: Option 'A' is correct.
Explanation:
Since we have given that
Probability of occurring of event A = 0.3
Probability of occurring of event B = 0.4
Since event A and B are independent events,
So,
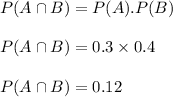
As we know the probability rules :
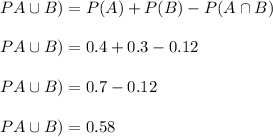
We need to find the probability that neither A or B occurs:
So,

Hence, Probability that neither A or B occurs is 0.42.
Therefore, Option 'A' is correct.