Question

Event A has a 0.3 probability of occurring and event B has a 0.4 probability of occurring. A and B are independent events. What is the probability that neither A or B occurs?

A. 0.42
B. 0.12
C. 0.10
D. 0.70

Answer 1

Answer: Option 'A' is correct.

Explanation:

Since we have given that

Probability of occurring of event A = 0.3

Probability of occurring of event B = 0.4

Since event A and B are independent events,

So,

`P(A\cap B)=P(A).P(B)\\\\P(A\cap B)=0.3* 0.4\\\\P(A\cap B)=0.12`

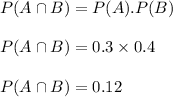
As we know the probability rules :

`PA\cup B)=P(A)+P(B)-P(A\cap B)\\\\PA\cup B)=0.4+0.3-0.12\\\\PA\cup B)=0.7-0.12\\\\PA\cup B)=0.58`

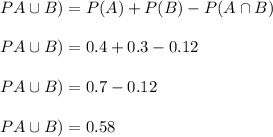
We need to find the probability that neither A or B occurs:

So,

`P(A'\cup B')=1-P(A\cup B)\\\\P(A'\cup B')=1-0.58\\\\P(A'\cup B')=0.42`

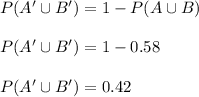
Hence, Probability that neither A or B occurs is 0.42.

Therefore, Option 'A' is correct.

Answer 2

The correct answer is A. 0.42

Explanation:

Probability that neither A nor B occurs

`= P(\bar{A})\cdot P(\bar{B})\\= (1 - 0.3)\cdot (1 - 0.4)\\= 0.7 \cdot 0.6\\ = 0.42`

Hence, the required probability is 0.42 and the correct option is A