Answer:
The ball touches the ground in a time t = 3.02 seconds.
Explanation:
We have the height equation as a function of time:
h = 182−12t-16t² Equation (1)
The height is equal to zero when the ball touches the ground.
Then we replace h = 0 in equation (1) to calculate the time in which the ball touches the ground:
0 = 182−12t-16t²
16t²+ 12t -182 = 0: Quadratic equation
We solve the quadratic equation to calculate t:
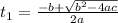
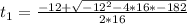
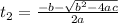
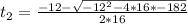
a = 16, b = 12, c = -182
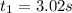
We take only the positive value for time because negative time does not exist,then,the ball touches the ground in a time t = 3.02 seconds.