Question

A ball is thrown from a height of 182 feet with an initial downward velocity of 12/fts. The ball's height h (in feet) after t seconds is given by the following. h=182−12t-16t^2

How long after the ball is thrown does it hit the ground?
Round your answer(s) to the nearest hundredth.

Answer 1

-3.768467990 , 3.018467990 <--- Answer, disregard the negative.

Answer 2

The ball touches the ground in a time t = 3.02 seconds.

Explanation:

We have the height equation as a function of time:

h = 182−12t-16t² Equation (1)

The height is equal to zero when the ball touches the ground.

Then we replace h = 0 in equation (1) to calculate the time in which the ball touches the ground:

0 = 182−12t-16t²

16t²+ 12t -182 = 0: Quadratic equation

We solve the quadratic equation to calculate t:

`t_(1) =\frac{-b+\sqrt{b^(2)-4ac } }{2a}`

`t_(1) =\frac{-12+\sqrt{-12^(2)-4*16*-182 } }{2*16}`

`t_(2) =\frac{-b-\sqrt{b^(2)-4ac } }{2a}`

`t_(2) =\frac{-12-\sqrt{-12^(2)-4*16*-182 } }{2*16}`

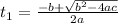
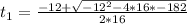
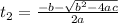
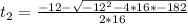
a = 16, b = 12, c = -182

`t_(1) =3.02 s`

`t_(2) =-3.76 s`

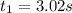
We take only the positive value for time because negative time does not exist,then,the ball touches the ground in a time t = 3.02 seconds.