Answer:
r = 2.8524 x10⁷ m = 28524 km
Step-by-step explanation:
First, we calculate the angular speed of the satellite:

Now, we use the formula for the gravitational force. Since gravitational force will be acting as the centrifugal force due to circular motion. Therefore,
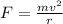
where,
F = Gravitational Forc = 105 N
m = mass of satellite = 40.9 kg
v = linear speed of satellite = rω = r(3 x 10⁻⁴ rad/s)
r = radius of orbit = ?
Therefore,
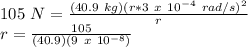
r = 2.8524 x10⁷ m = 28524 km