Question

If cos2 x + 2cosx - 2 = 0, then cosx = _____.

A. -1 ± sqrt 3
B. 1 ± sqrt 3
C. ± sqrt 3
D. 1

Answer 1

assuming cos2 x means cos^2 x, u can substitute y=cosx and the equation becomes: y^2 + 2y -2 =0

solving it gives the solution -1+-sqrt(3)

Answer 2

Option D. 1

Explanation:

Thinking process:

Let the quadratic equation be given by the formula:

`cos^(2) x+ 2 cosx - 2 = 0`

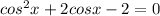
then solving the equation using the factorization method:

using the trigonometry identity of cos 2x

then

`Cos2x = 2cos^(2)x - 1`

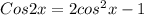
Substituting 2Cos²x - 1 gives:

2
`cos^(2) x-1+cos^(2)x-2= 0`

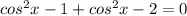
rearranging gives:

`3cos^(2)x = 3\\ cosx = √(1) \\ = 1`

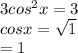
hence cosx = 1