Question

Martina made deposits of $2,000 at the beginning of each year for four years. The rate she earned is 5% annually. What's the value of Marina's account in four years? A. $11,051.00 B. $9,051.20 C. $8,260.00 D. $8,260.20

Answer 1

i think B. $9,051.20 is the answer

Answer 2

The value of Marina's account in four years is $ 9051.42 .

Option (B) is correct .

Explanation:

Formula for future value of annuity .

`FV_(Annuity\ Due) = C* ((1+i)^(n)-1)/(i)* (i+1)`

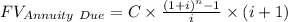
Where C is the cash flow per period , i is the rate of interest and n is the number of payments .

As given

Martina made deposits of $2,000 at the beginning of each year for four years. The rate she earned is 5% annually.

C = $2000

5% is written in the decimal form .

`= (5)/(100)`

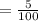
= 0.05

i = 0.05

n = 4

Putting all the values in the above formula

`FV_(Annuity\ Due) = 2000* ((1+0.05)^(4)-1)/(0.05)* (0.05+1)`

`FV_(Annuity\ Due) = 2000* ((1.05)^(4)-1)/(0.05)* (1.05)`

`FV_(Annuity\ Due) = 2000* ((1.05)^(4)-1)/(0.05)* (1.05)`

`FV_(Annuity\ Due) = 2000* (1.21551-1)/(0.05)* (1.05)`

`FV_(Annuity\ Due) = 2000* (0.21551)/(0.05)* (1.05)`

`FV_(Annuity\ Due) = 2000* 4.3102* (1.05)`

`FV_(Annuity\ Due) = \$ 9051.42`

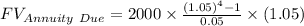
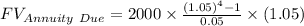
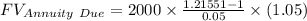
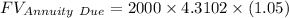
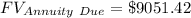
Therefore the value of Marina's account in four years is $ 9051.42 .

Option (B) is correct .