Answer:
The value of Marina's account in four years is $ 9051.42 .
Option (B) is correct .
Explanation:
Formula for future value of annuity .
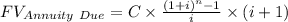
Where C is the cash flow per period , i is the rate of interest and n is the number of payments .
As given
Martina made deposits of $2,000 at the beginning of each year for four years. The rate she earned is 5% annually.
C = $2000
5% is written in the decimal form .
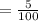
= 0.05
i = 0.05
n = 4
Putting all the values in the above formula
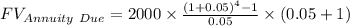
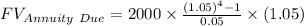
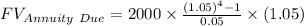
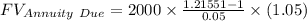
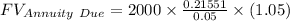
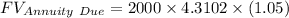
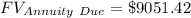
Therefore the value of Marina's account in four years is $ 9051.42 .
Option (B) is correct .