Alice wants to know how much she'll invest today to receive an annuity of $10,000 for six years if interest is earned at 7% annually.
We will use Annuity Payment formula, which states:

where P is the payment,
PV is the present value,
r= rate per period,
n=number of periods.
According to the question,
P = $10,000
r=7%
n=6
We have to find the present value,
Substituting the values in the given formula,
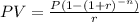
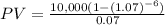
PV= $ 47,665.
So, Alice wants to invest $47,665 today to receive an annuity of $10,000 for six years if interest is earned at 7% annually.