Question

The rectangle shown has a perimeter of 34 cm and the area given its length is 5 more than twice the width write and solve a system of equations to find the dimensions of the rectangle a=52cm^2

Answer 1

2(2w+5) + 2W =34
4w+10+2w=34
6W+10=34
-10 -10
6w=24
Width =4
Length =13

Answer 2

The width and the length of rectangle are 4 cm and 13 cm respectively .

Explanation:

Let the width be x

We are given that its length is 5 more than twice the width

So, length= 2x+5

Perimeter of rectangle =
`2(L+W)`

=
`2(x+2x+5)`

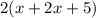
We are given that perimeter is 34 cm

So,
`2(x+2x+5)= 34`

`6x+10= 34`

`6x= 24`

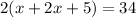
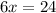
x=4

So, width = 4 cm

Length = 2x+5=2(4)+5=13 cm

Area of rectangle =
`Length * width = x(2x+5)`

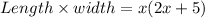
We are given that area is 52sq.cm

So,
`x(2x+5) =52`

`2x^2+5x=52`

`(x-4)(2x+13)=0`

`x=4,(-13)/(2)`

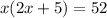
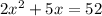
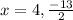
Since width cannot be negative

So,width = 4 cm

Length = 2x+5=2(4)+5=13 cm

Hence The width and the length of rectangle are 4 cm and 13 cm respectively .