Answer:
The width and the length of rectangle are 4 cm and 13 cm respectively .
Explanation:
Let the width be x
We are given that its length is 5 more than twice the width
So, length= 2x+5
Perimeter of rectangle =
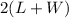
=
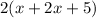
We are given that perimeter is 34 cm
So,
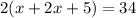
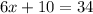
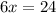
x=4
So, width = 4 cm
Length = 2x+5=2(4)+5=13 cm
Area of rectangle =
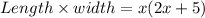
We are given that area is 52sq.cm
So,
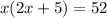
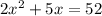
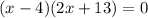
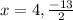
Since width cannot be negative
So,width = 4 cm
Length = 2x+5=2(4)+5=13 cm
Hence The width and the length of rectangle are 4 cm and 13 cm respectively .