Answer:
Answer is explained in the explanation section.
Step-by-step explanation:
A)
Solution:
For this to find, we need to calculate the centripetal acceleration on the equator.
The centripetal acceleration of the equator:
a = 4
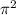 RcosФ/
RcosФ/
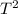 ,
,
where,
R is the radius of the earth
R = 6378 KM = 6.3 x
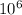 and
and
T is the time period
T = 24 h = 86164.1 s
At Equator, Ф = 0°
So, CosФ = 1
Hence,
a = 4
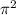 R/
R/
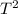
By plugging in the values, we get:
a = 4 x (
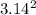 ) x (6.3 x
) x (6.3 x
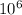 ) /
) /
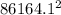
a = 0.03 m/
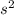
Hence, this is the centripetal acceleration on the equator. And we also know that, acceleration due to gravity is 9.8 m/
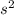 which is very higher than the centripetal acceleration on the equator.
which is very higher than the centripetal acceleration on the equator.
B) Normal force exerted by chair will always be equal and opposite to the mass times gravitational acceleration (F = mg). Otherwise, I would be thrown away from chair in case the normal force is not equal and opposite or I would be drag down to the earth due to greater mass times gravitational acceleration. Hence, both are equal and opposite.
C) Of course, this is not a lie, it is true because the acceleration due to gravity is 9.8 m/
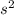 and as we calculated the acceleration on the equator is 0.03 m/
and as we calculated the acceleration on the equator is 0.03 m/
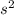 which way too low to experience.
which way too low to experience.
For percentage difference,
9.8 - 0.03 = 9.77
So, % diff = (9.8 - 9.77)/9.8 x 100
% diff = 0.00306 x 100
% diff = 0.306%
Obviously, this is way too low to experience.
D) With the help of same formula as discussed above, we have:
a = 4
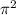 RcosФ/
RcosФ/
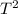 ,
,
Here, Ф = 44.4°
Just putting the values. we get
a = 0.0241 m/
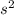
Acceleration while sitting in my chair.