Question

So far in your life, you may have assumed that as you are sitting in your chair right now, you are not accelerating. However, this picture is not quite complete! You are on the surface of the Earth, which is rotating.

A) What is the acceleration of a person sitting in a chair on the equator?
B) At the equator, is your mass times the gravitational acceleration of the Earth greater than, less than, or equal to the normal force exerted on you by the chair you are sitting on? Explain.
C) A classmate of yours asks you why we have ignored this acceleration for the whole first term of physics. "Is everything we've learned a lie?" they ask. Assuage their fears by calculating the percent- age difference between the normal force from the chair and your weight while sitting on equator.
D) The latitude of Corvallis is 44.4'. What is your acceleration while sitting in your chair?

Answer 1

Answer is explained in the explanation section.

Step-by-step explanation:

A)

Solution:

For this to find, we need to calculate the centripetal acceleration on the equator.

The centripetal acceleration of the equator:

a = 4
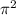`\pi ^(2)`RcosФ/
`T^(2)`,

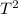where,

R is the radius of the earth

R = 6378 KM = 6.3 x
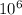`10^(6)` and

T is the time period

T = 24 h = 86164.1 s

At Equator, Ф = 0°

So, CosФ = 1

Hence,

a = 4
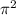`\pi ^(2)`R/
`T^(2)`

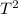
By plugging in the values, we get:

a = 4 x (
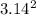`3.14^(2)`) x (6.3 x
`10^(6)`) /
`86164.1^(2)`

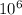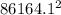
a = 0.03 m/
`s^(2)`

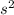
Hence, this is the centripetal acceleration on the equator. And we also know that, acceleration due to gravity is 9.8 m/
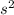`s^(2)` which is very higher than the centripetal acceleration on the equator.

B) Normal force exerted by chair will always be equal and opposite to the mass times gravitational acceleration (F = mg). Otherwise, I would be thrown away from chair in case the normal force is not equal and opposite or I would be drag down to the earth due to greater mass times gravitational acceleration. Hence, both are equal and opposite.

C) Of course, this is not a lie, it is true because the acceleration due to gravity is 9.8 m/
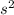`s^(2)` and as we calculated the acceleration on the equator is 0.03 m/
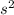`s^(2)` which way too low to experience.

For percentage difference,

9.8 - 0.03 = 9.77

So, % diff = (9.8 - 9.77)/9.8 x 100

% diff = 0.00306 x 100

% diff = 0.306%

Obviously, this is way too low to experience.

D) With the help of same formula as discussed above, we have:

a = 4
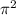`\pi ^(2)`RcosФ/
`T^(2)`,

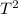Here, Ф = 44.4°

Just putting the values. we get

a = 0.0241 m/
`s^(2)`

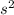
Acceleration while sitting in my chair.