Answer:
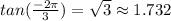
Explanation:
First of all let's define the tangent function:
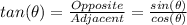
Now, let's define the standard angles, standard angles are those that have values that appear very often in everyday life. These angles are 30°=π/6, 45°=π/4, and 60°=π/3, and the angles 0°, 90°=π/2, 120°= 2π/3, 180°=π, 270°=3π/2, and 360°=2π. The latter, although not defined as 'standard', are also very common. Here are the values:
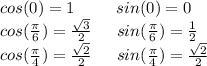
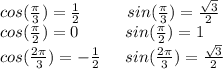
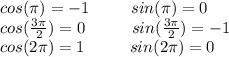
Also you need to keep in mind that cosine function is an even function, and sine function is an odd function, that is:
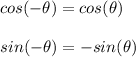
Using these definitions you are able to solve the problem:
