Question

Look at the graph below Which part of the graph best represents the solution set to the system of inequalities y ≥ x + 1 and y + x ≥ −1

Answer 1

The solution set of given inequalities are represented by Part A.

Explanation:

The given inequalities are

`y\geq x+1`

`y+x\geq -1`

The related equations of both inequalities are

`y=x+1`

Put x=0, to find the y-intercept and put y=0, to find x intercept.

`y=0+1\Rightarrow y=1`

`0=x+1\Rightarrow x=-1`

Therefore x-intercept of the equation is (-1,0) and y-intercept is (0,1).

Similarly, for the second related equation

`y+x=-1`

`y+0=-1\Rightarrow y=-1`

`0+x=-1\Rightarrow x=-1`

Therefore x-intercept of the equation is (-1,0) and y-intercept is (0,-1).

Now, join the x and y-intercepts of both lines to draw the line.

Now check the given inequalities by (0,0).

`0\geq 0+1\Rightarrow 0\geq 1`

It is a false statement, therefore the shaded region is in the opposite side of origin.

`0+0\geq -1\Rightarrow 0\geq -1`

It is a true statement, therefore the shaded region is about the origin.

From the below figure we can say that the solution set of given inequalities are represented by Part A.

Answer 2

ANSWER

Part A

EXPLANATION

The given inequalities are,


`y \geqslant x + 1`

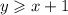
and


`y + x \geqslant - 1`

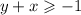
To see which part of the graph best represent the solution set, choose a point from each part and substitute in to the inequalities.

If a point from a given part satisfies the inequalities simultaneously, then that part best represents the solution set.

Part A.

We choose

`(0,2)`
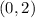
We plug in to the inequalities.


`2 \geqslant 0 + 1`


`\Rightarrow \: 2 \geqslant 1`
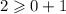
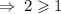
The above inequality is true.

We plug in to the second inequality.


`2 + 0 \geqslant - 1`

.

`\Rightarrow \: 2 \geqslant - 1`

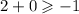
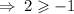
This statement is also true.

Part B.

If we plug in

`(-2,0)`
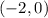
in to the first statement, we get,


`0 \geqslant - 2 + 1`

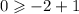
This implies that,


`0 \geqslant - 1`

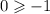
This is true.

If substitute in to the second, we get,


`0 + - 2\geqslant - 1`


`\Rightarrow \: - 2 \geqslant - 1`
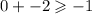
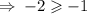
This is false.

Part C

We plug

`(0,-2)`
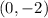
in to the first inequality


`- 2 \geqslant 0 + 1`
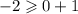
This means that,


`- 2 \geqslant 1`
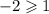
This is false.

We plug in to the second inequality,


`- 2 + 0 \geqslant -1`


`- 2 \geqslant -1`

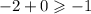
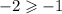
False.

Part D also has the point


`(2,0)`

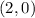
We put this point in to the first inequality to get,


`0 \geqslant 2 + 1`

`0 \geqslant 3`
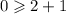
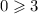
This is false.

Then in to the second inequality.


`0 + 2 \geqslant 1`

`2 \geqslant -1`

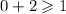
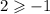
This final statement is true.

Since the point from Part A satisfies both inequalities simultaneously, it represents the solution set.