Question

Solve the logarithmic equation. When necessary, round answer to the nearest hundredth. log 5 x + log 5(2x + 3) = 1

Answer 1

X is equivalent to 1 since x cannot take negative value

Answer 2

Answer: The required solution is x = 1.

Step-by-step explanation: We are given to solve the following logarithmic equation :

`\log_5x+\log_5(2x+3)=1~~~~~~~~~~~~~~~~~~~~~~~~~~~~(i)`

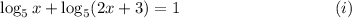
We will be using the following logarithmic properties in solving the given equation :

`(i)~\log_ab+\log_ac=\log_abc,\\\\(ii)~\log_ab=c~~~~~\Rightarrow b=a^c.`

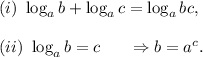
From equation (i), we have

`\log_5x+\log_5(2x+3)=1\\\\\Rightarrow \log_5\{x(2x+3)\}=1\\\\\Rightarrow \log_5(2x^2+3x)=1\\\\\Rightarrow 2x^2+3x=5^1\\\\\Rightarrow 2x^2+3x=5\\\\\Rightarrow 2x^2+3x-5=0\\\\\Rightarrow 2x^2+5x-2x-5=0\\\\\Rightarrow x(2x+5)-1(2x+5)=0\\\\\Rightarrow (x-1)(2x+5)=0\\\\\Rightarrow x-1=0,~~~~~2x+5=0\\\\\Rightarrow x=1~~~~~~~\Rightarrow x=-(5)/(2).`

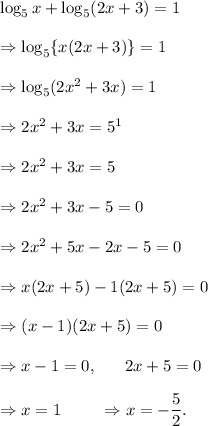
Since the logarithm of a negative number does not exist, so we get

x = 1.

Thus, the required solution is x = 1.