Answer: The required solution is x = 1.
Step-by-step explanation: We are given to solve the following logarithmic equation :
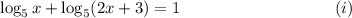
We will be using the following logarithmic properties in solving the given equation :
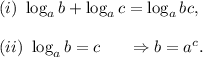
From equation (i), we have
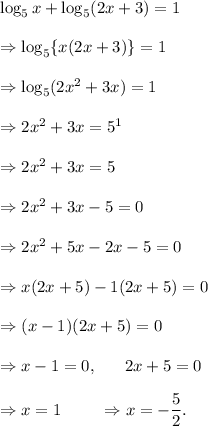
Since the logarithm of a negative number does not exist, so we get
x = 1.
Thus, the required solution is x = 1.