Question

What is the derivative of square root of 2x?

Answer 1

`\displaystyle (d)/(dx)[√(2x)] = (√(2))/(2√(x))`

General Formulas and Concepts:

Calculus

Differentiation

• Derivatives
• Derivative Notation

Derivative Property [Multiplied Constant]:
`\displaystyle (d)/(dx) [cf(x)] = c \cdot f'(x)`

Basic Power Rule:

1. f(x) = cxⁿ
2. f’(x) = c·nxⁿ⁻¹

Derivative Rule [Chain Rule]:
`\displaystyle (d)/(dx)[f(g(x))] = f'(g(x)) \cdot g'(x)`

Explanation:

Step 1: Define

Identify

`\displaystyle y = √(2x)`

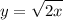
Step 2: Differentiate

1. Basic Power Rule [Derivative Rule - Chain Rule]:
   `\displaystyle (dy)/(dx) = (1)/(2√(2x)) \cdot (d)/(dx)[2x]`
2. Basic Power Rule [Derivative Property - Multiplied Constant]:
   `\displaystyle (dy)/(dx) = (2)/(2√(2x))`
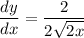
3. Simplify:
   `\displaystyle (dy)/(dx) = (1)/(√(2x))`

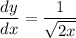
Topic: AP Calculus AB/BC (Calculus I/I + II)

Unit: Differentiation