Answer:
![\displaystyle (d)/(dx)[√(2x)] = (√(2))/(2√(x))](https://img.qammunity.org/2019/formulas/mathematics/high-school/eht68iv6vjwrn1fp8bkihz9sblslel99je.png)
General Formulas and Concepts:
Calculus
Differentiation
- Derivatives
- Derivative Notation
Derivative Property [Multiplied Constant]:
![\displaystyle (d)/(dx) [cf(x)] = c \cdot f'(x)](https://img.qammunity.org/2019/formulas/mathematics/high-school/h3h81fknzks3m5lkzvmdwrmpof8mpsbacs.png)
Basic Power Rule:
- f(x) = cxⁿ
- f’(x) = c·nxⁿ⁻¹
Derivative Rule [Chain Rule]:
![\displaystyle (d)/(dx)[f(g(x))] = f'(g(x)) \cdot g'(x)](https://img.qammunity.org/2019/formulas/mathematics/high-school/hgp8e7za5sb149n4p44jnz94ansi74e49t.png)
Explanation:
Step 1: Define
Identify
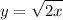
Step 2: Differentiate
- Basic Power Rule [Derivative Rule - Chain Rule]:
![\displaystyle (dy)/(dx) = (1)/(2√(2x)) \cdot (d)/(dx)[2x]](https://img.qammunity.org/2019/formulas/mathematics/high-school/qwm5nzata1subjfe0i0njgyxzpzh3e3kil.png)
- Basic Power Rule [Derivative Property - Multiplied Constant]:
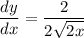
- Simplify:
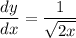
Topic: AP Calculus AB/BC (Calculus I/I + II)
Unit: Differentiation