Question

Which is the equation of a parabola with focus (0, 5) and directrix y= -5?

Answer 1

As the focus is at (0,5) it will be symmetrical about the y axis and will open upwards

General formula is x^2 = 4ay where a is the y coordinate of the focus

So its y = x^2/5*4

y = 1/20 x^2

Answer 2

Answer: Our require equation of parabola is given by

`x^2=20y`

Explanation:

Since we have given that

Focus (0,5) -------------(1)

And we know that the general form of focus is given by

Focus (h,k+p) -------------------(2)

So, Comparing both the equations we get that

h = 0

and k+p = 5 ----------------------(3)

And directrix is given by

y = -5

The general form of directrix is given by

y = k-p

Putting the value of y in the above equation :

-5=k-p

p-k=5 ----------------------------(4)

Using (3) and (4), we get that

`p-k=k+p\\\\0=2k\\\\k=0`

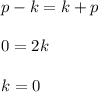
So, putting the value of k in equation (3), we get that

`p=5`

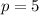
So, the equation of parabola becomes,

`(x-h)^2=4p(y-k)\\\\x^2=4* 5y\\\\x^2=20y`

Hence, our require equation of parabola is given by

`x^2=20y`