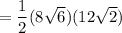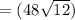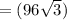Question

Identify the perimeter and area of an equilateral triangle with height 12√2cm. Give your answer in simplest radical form. PLEASE HELP ASAP!!

Answer 1

Answer: (D) P=24√6, A=96√3

Explanation:

Consider ΔABC where D is the midpoint of BC. Since ABC is an equilateral triangle, then segment AD is a perpendicular bisector with length of 12√2. This creates ΔADC which is a 30°-60°-90° triangle.

Now you can use the rules for this special triangle to find the length of the hypotenuse.

30° ⇄ side length "a" base - DC on ΔADC

60° ⇄ side length "a√3" height - AD on ΔADC

90° ⇄ side length "2a" hypotenuse - AC on ΔADC

Step 1: solve for "a"

`AD: a\sqrt3=12√(12)`

`(a\sqrt3)/(\sqrt3)=(12\sqrt2)/(\sqrt3)`

`a=(12\sqrt2)/(\sqrt3)\bigg((√(3))/(√(3))\bigg)`

`= (12\sqrt6)/(3)`

`=4\sqrt6`

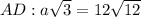
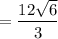
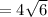
Step 2: solve for "2a"

`AC: 2a =2(4√(6))`

`=8√(6)`

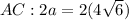
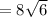
Step 3: find the perimeter

The side length is equivalent for all 3 sides so

P = 3(AC)

`=3(8√(6))`

`=24√(6)`

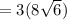
Step 4: find the area

`A=(1)/(2)b \cdot h`

`=(1)/(2)(8\sqrt6)(12\sqrt2)`

`=(48√(12))`

`=(96\sqrt3)`