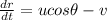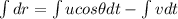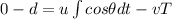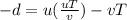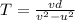Let after time "t" the Position of A and B are in such a way that A is heading to B and its velocity makes some angle with x axis
So the relative speed of A with respect to B in horizontal direction is given as
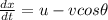
relative motion in y direction is given as
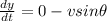
from first equation we can say
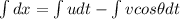
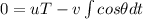

now in the direction of approach of each other