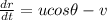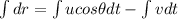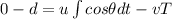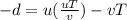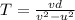Question

Two particles A and B are initially at distance d apart. They start moving simultaneously at velocity v and u such that A always move towards B and B moves along fixed straight line which is perpendicular to initial direction of motion of A. Then particles will meet after time

A. (vd)/(v^2-u^2)
B. (ud)/(u^2-v^2)
C. d/(v^2+u^2)^1/2
D. vd/(v^2+u^2)

Answer 1

Let after time "t" the Position of A and B are in such a way that A is heading to B and its velocity makes some angle with x axis

So the relative speed of A with respect to B in horizontal direction is given as

`(dx)/(dt) = u - vcos\theta`

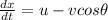
relative motion in y direction is given as

`(dy)/(dt) = 0 - vsin\theta`

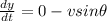
from first equation we can say

`\int dx = \int u dt - \int vcos\theta dt`

`0 = uT - v\int cos\theta dt`

`\int cos\theta dt = (uT)/(v)`

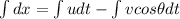
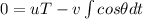
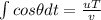
now in the direction of approach of each other

`(dr)/(dt) = ucos\theta - v`

`\int dr = \int ucos\theta dt - \int vdt`

`0 - d = u\int cos\theta dt - vT`

`- d = u((uT)/(v)) - vT`

`T = (vd)/(v^2 - u^2)`