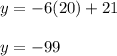Question

Find the 20th term of the arithmetic sequence

Answer 1

First we must look at the sequence 15,9,3,-3...

You can see that the value is decreasing by 6 every term. Because the rate is drawing at a constant rate the sequence must be linear, meaning that the slope is -6.

If we look at the general function of a line in slope intercept form:


`y = mx + b`
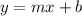
where m is the slope and b is the y intercept. The trick to find the y intercept is to go backwards, in other words what was the previous term? 15+6=21. Therefore, m=-6 and b=21 and thus,


`y = - 6 x+ 21`
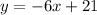
Since we want to know the value of y even x=20 we obtain:


`y = - 6(20) + 21 \\ \\ y = - 99`

Answer 2

-99

Explanation:

Given :

Arithmetic sequence : 15 , 9 ,3 , -3 , ........

To Find : 20th term .

Solution :

Formula of nth term in Arithmetic mean :
`a_(n) = a+(n-1)*d` ---(A)

where

a = first term of sequence

n = term position

d = common difference

`a_(n)` = the term you want to find

Thus in the given sequence:

a = 15 ( first term )

n = 20 th term ( given )

d = 9-15 = 3-9 = -6(common difference)

Putting values in (A)

⇒
`a_(20) = 15+(20-1)*(-6)`

`a_(20) = 15-114`

`a_(20) = -99`

Hence the 20th term is -99 i.e. option 1