Question

A and B are complementary angles. If m_A = (6x + 29) and m

B = (x + 5)', then find the measure of A.

Answer 1

The measurement of angle A is: 77°

Explanation:

First of all, let us define complementary angles

The angles whose sum is 90° are called complementary angles.

Given angles are:

m∠A = 6x+29

m∠B = x+5

With respect to the definition, the sum of both angles will be 90°

Writing this mathematically we get

`A+B = 90\\6x+29+x+5 = 90\\7x+34=90\\7x = 90-34\\7x = 56\\(7x)/(7) = (56)/(7)\\x = 8`

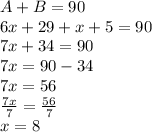
Putting the value of x in the expression for angle A

`A = 6x+ 29 = 6(8)+29 =48+29\\A = 77`

Hence,

The measurement of angle A is: 77°

Answer 2

m∠
`A=77`°

Explanation:

Complementary angles are a pair of angles whose measures have a sum of
`90`°. Since m∠
`A` =
`6x+29` and m∠
`B` =
`x+5`, we can write the following equation to solve for
`x`:

`6x+29+x+5=90`

Solving for
`x`, we get:

`6x+29+x+5=90`

`7x+34=90` (Simplify LHS)

`7x+34-34=90-34` (Subtract
`34` from both sides of the equation to isolate
`x`)

`7x=56` (Simplify)

`(7x)/(7)=(56)/(7)` (Divide both sides of the equation by
`7` to get rid of
`x`'s coefficient)

`x=8`

Therefore, m∠
`A=6x+29=6(8)+29=48+29=77`°. Hope this helps!