Question

The first term if an arithmetic sequence is -5 and the tenth term is 13. Find the common difference.

Answer 1

`\bf n^(th)\textit{ term of an arithmetic sequence} \\\\ a_n=a_1+(n-1)d\qquad \begin{cases} n=n^(th)\ term\\ a_1=\textit{first term's value}\\ d=\textit{common difference}\\[-0.5em] \hrulefill\\ a_1=-5\\ n=10\\ a_(10)=13 \end{cases} \\\\\\ a_(10)=a_1+(10-1)d\implies 13=-5+(10-1)d \\\\\\ 13=-5+9d\implies 18=9d\implies \cfrac{18}{9}=d\implies 2=d`

Answer 2

Common difference = 2

Explanation:

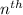`n^(th)` term of an arithmetic progression is given by a + (n-1)d, where a is the first term and d is the common difference.

Here first term is given as -5

a = -5

Tenth term is 13

n = 10

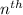`n^(th)` term = 13

We have

-5 + (10-1)d = 13

9 d = 13 + 5

9 d = 18

d = 2

Common difference = 2