Answer:
The point of inflection is (1,9)
Explanation:
We have following given function
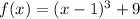
The point at which the function changes its curvature is defined by the point of inflection.
To find point of inflection we set 2nd derivative to 0
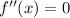
The first derivative is given by
![f'(x)= (d)/(dx) [(x-1)^(3) +9]](https://img.qammunity.org/2019/formulas/mathematics/high-school/igl1306f09l72m7p3ndzpnunfkv4p55nua.png)
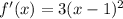 ( using chain rule and derivative of constant is 0)
( using chain rule and derivative of constant is 0)
now again we take 2nd derivative
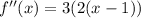
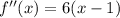
now we equate 2nd derivative to 0
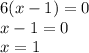
hence point of inflection is at x=1
now we find y coordinate of point of inflection by plugging x=1 in f(x)
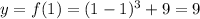
Hence the point of inflection is (1,9)