Answer:
(1)
option-B
(2)
f(x) is continuous at a=4
Explanation:
(1)
we are given

Since, we are suppose to find limit x-->0
so, we always choose value of x that is close to 0
At x=-0.03:

At x=-0.02:
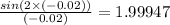
At x=-0.01:

At x=0.01:
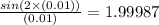
At x=0.02:
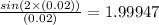
At x=0.03:
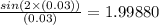
(2)
we are given
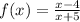
Since, we have to check continuity at a=4
So, firstly we will find limit value and then functional value
Limit value:
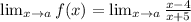
now, we can plug a=4
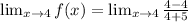
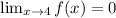
Functional value:
We can plug x=4 into f(x)

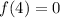
So, we can see that

So, limit value is equal to function value
so, f(x) is continuous at a=4.............Answer