Question

DHL Shipping claims that it ships 95% of its orders within three working days. You select a simple random sample of 100 orders and discover that only 91 of them shipped on time.

a) If DHL really does ship 95% on time, what is the probability that the company shipped 91 or fewer out of 100 orders were shipped on time?

b) A marketer from UPS jumps on the research stating, "They claim 95% on time, but by their own research they only ship 91% on time!" Provide a rebuttal to the UPS marketer in non-statistical terms.

Answer 1

a) 5.4%

Explanation:

a) We will use the binomial distribution, with n = 100 and p(success) = 0.95

We need to calculate

P(X=x) =
`\binom{n}{x}p^(x)q^(n-x)`

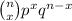
P(X ≤91) =
`\sum_(k=1)^(91)\binom{100}{k}0.95^(k)0.5^(n-k)`

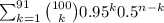
As we know that binomial distribution can be approximated to normal distribution if np≥5 and nq≥5 as in this case.

Therefore, P(x,n,p) →N
`(\mu, \sigma )`

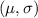
`\mu` = np = 95

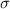`\sigma` = √npq = 2.`79

P(X≤91) ≅ P(X≤91.5) = P( Z≤
`(91.5-95)/(2.179)`

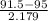
= P( Z≤ -1.6)

= 0.054

Probability = 5.4%

b) If the probability was less than 5% then we must say that the DHL Shipping company don not ships 95% of its orders on time but as we can see that the probability is more that 5% that is 5.4%. So, we cannot say that the company does not ships the orders on time. But we cannot say with confirmation, we need more samples so as to judge accordingly.